Approximating π
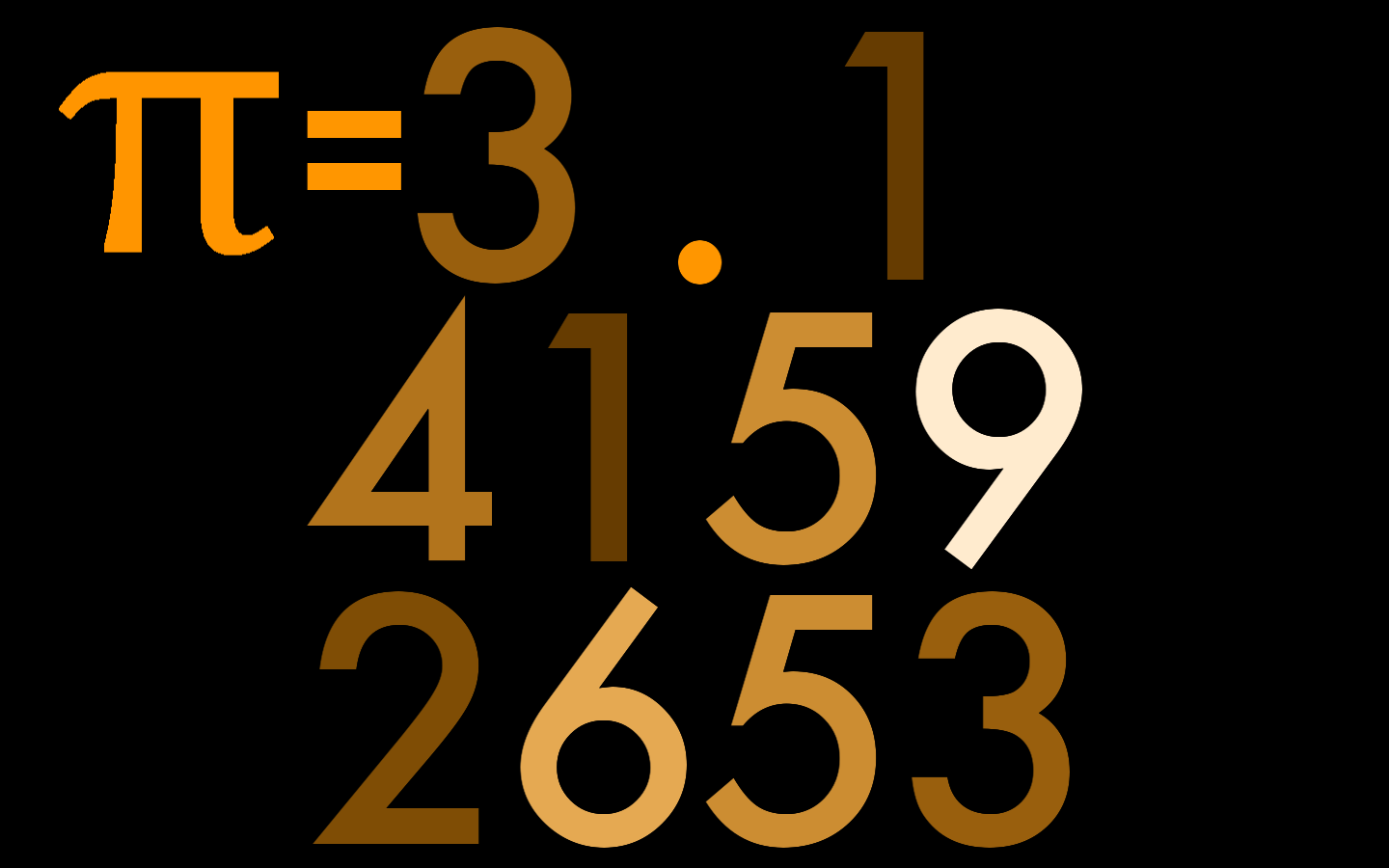
Approximating π is a computer music composition by Clarence Barlow that was based on the sonification of the digits of π. It derives various aspects of the composition from the following series approximation:
At his request, Matthias Wagner and I had the opportunity to implement this piece to synthesize sound and produce visuals using his original program notes from 2007 to put together the first ever performance of this piece with multi-channel visuals.
Each channel approximates π at a different rate, all the channels together form a harmonic series based on a formula involving π). The whole piece is conceptualized such that it can be flexibly played on up to 16 A/V channels, and for any duration up to 1.5 years. The longest it has run till date is 2 hours, with 6-channels (6 monitors + 6 speakers).
Implementation Highlights:
- Implemented in C++ using OpenFrameworks
- Synthesizes multichannel audio (2-, 4-, 8- or 16- channels)
- Synthesizes multichannel video over multiple-monitors (one for each audio channel)
- Distributed – can run synchronously on multiple machines (uses OSC)



Approximating π was exhibited using our software implementation both as an art installation and in a concert setting at the following venues.
| 2016, July 12 | BAR70W, Conservatory for New Music, Köln, Germany |
| 2016, May 28 | "White Noise", SBCAST, Santa Barbara, CA |
| 2016, May 27 | "White Noise", Elings Hall, UCSB, Santa Barbara, CA |
| 2016, Apr 24 | Montage Concert, Lotte Lehman Concert Hall, Santa Barbara, CA |
Offshoots: With a little modification, this software was used to perform a spatialized rendition of Hector Berlioz’s Symphony Fantastique for a concert by graduate students of UCSB Music.
Composition by: Clarence Barlow.
Software: Akshay Cadambi and Matthias Wagner.
Code is available here.